Only released in EOL distros:
Package Summary
tf_uncertainty
- Author: Thomas Ruehr
- License: BSD
- Source: git https://github.com/ruehr/uncertain_tf.git (branch: None)
Package Summary
tf_uncertainty
- Author: Thomas Ruehr
- License: BSD
- Source: git https://github.com/ruehr/uncertain_tf.git (branch: None)
Contents
Introduction
uncertain_tf is an extension to tf that allows to maintain uncertainty in the translation and rotation of coordinate frames.
Design
There are many ways to introduce uncertainty to a system like tf, this section shall give an overview into the design decisions that were taken for uncertain_tf.
Uncertainty is modelled locally for each frame in form of a variance/covariance matrix defining a distribution in position and euler angles. The covariance matrixes are communicated similar to the transformations in the tf tree via a central topic tf_uncertainty. The messages contain a vector of stamped covariances, which is float64[36]. The header of the message contains a frame_id and a timestamp as usual.
Conventions
The variance defined relates to the coordinate frame it is defined for, meaning a variance in x on the base_link would mean that the robot location is uncertain but lies on a line along the robot's x axis. Seen from /map, all coordinates within frames that lie under the base_link will be affected by this uncertainty, while transforms between frames that both lie under base_link in the tree will not 'see' the uncertainty.
The rviz screenshots below show 50 samples each, taken from the distribution of the object pose relative to the map frame. On the left side an uncertainty in the x axis was defined with variance 0.1, in the object frame (top) and the base_link frame (bottom). On the right side, an uncertainty in rotation around the z axis of the frames was defined similarly.
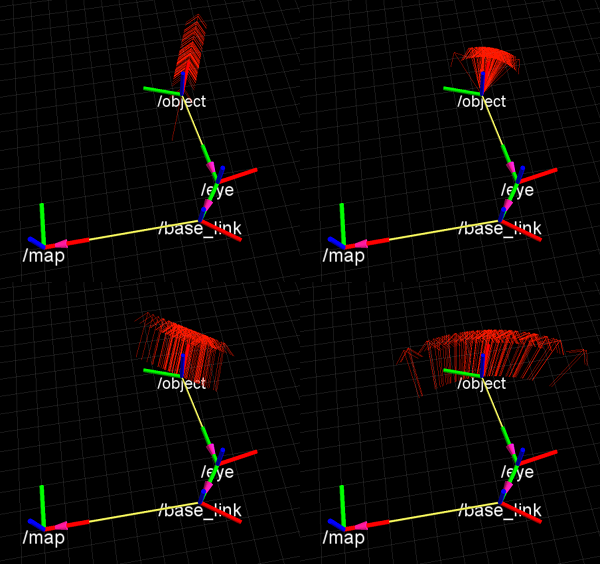
Sampling
Naturally, uncertainty in rotation will act as a nonlinear transformation on the probability distributions. Therefore, gaussian distributions are not able to reflect the shape of a distribution after a transformation through a frame with rotational uncertainty. To address this issue, an interface is defined that allows to sample transformations between two frames. Depending on the number of samples, the sample set will give a better idea of the actual probability distribution than a simple gaussian.
API
Creating a Stamped Covariance, in this example only containing a variance of 1m in x and 0.1 in rotation around z publishing it. Note: the UncertainTransformBroadcaster inherits from tf::TransformBroadcaster, so normal tf frames can as well be sent by it.
#include <uncertain_tf/UncertainTransformBroadcaster.h>
...
uncertain_tf::UncertainTransformBroadcaster utfb;
...
StampedCovariance stc;
stc.resize(6,6);
stc.setZero();
stc(0,0) = 1;
stc(4,4) = 1;
stc.frame_id_ = "/base_link";
stc.stamp_ = ros::Time::now();
utfb.sendCovariance(cov_to_send);Create 50 samples between two given frames at a given time:
UncertainTransformListener ulistener;
...
std::vector<tf::StampedTransform> transform_samples;
ulistener.sampleTransform("map", "object_on_table", ros::Time(0), transform_samples, 50);Calculate a gaussian distribution with mean and covariance for the samples created above and resample from it. Similar code can be used to estimate a covariance for a given sample set, e.g. of object poses. The resampling gives an idea of how bad a rerpresentation with a gaussian instead of samples would be.
MatrixXd sample_covar;
MatrixXd samples = ulistener.sampleSetTFtoMatrixXd(transform_samples);
ulistener.calculateSampleCovariance(samples, samples, sample_covar);
std::cout << "sample covariance " << endl << sample_covar << endl;
MatrixXd mean = ulistener.calculateSampleMean(samples);
std::cout << "sample mean" << endl << mean << endl;
std::vector<tf::Transform> resampled;
ulistener.sampleFromMeanCov(ulistener.transformVectorXdToTF(mean), sample_covar, resampled, 50);Create 50 samples for the transform between the given frames, sampling in time, here around 4 seconds in the past with 2 seconds variance. Note: sampling in time can bring up times that are either in the future or outside of the tf cache. In these cases, the exceptions are caught but no sample is generated for these times. As a result, the sampleset will be smaller, e.g. transform_samples may contain only 30 transforms instead of the 50 asked for.
std::vector<StampedTransform> transform_samples;
ulistener.sampleTransformGaussianTime("map", "object_on_table", ros::Time::now() - ros::Duration(4),ros::Duration(2), transform_samples, 50);Create 50 samples for the transform between the given samples, with uniform time steps between a start and end time, here 4 seconds in the past till 2 seconds in the past. This can be useful to see how sensor data is affected by time error, such as asking where the object could be if there was +-.03s shutter to time stamp offset.
std::vector<StampedTransform> transform_samples;
ulistener.sampleTransformUniformTime("map", "object_on_table", ros::Time::now() - ros::Duration(4),ros::Time::now() - ros::Duration(2), transform_samples, 50);
Math
Simply put, calculating Covariance Matrices from Euler Angles is not the best way to look at uncertainty in Rotation and it's propagation. We are currently looking into how to implement this package in a more canonical way.
= Tools = Static covariance and variance publishers are available as well as a visualization component that samples n transforms and publishes them as a pose array message.
The static variance publisher will only populate the diagonal of the covariance matrix:
rosrun uncertain_tf static_variance_publisher USAGE: static_variance_publisher frame_id var_x var_y var_z var_rot_z var_rot_y var_rot_x period(milliseconds)
The static covariance publisher takes in a full covariance matrix:
rosrun uncertain_tf static_covariance_publisher
USAGE: static_covariance_publisher frame_id var_x cov_xy cov_xz cov_xZ cov_xY cov_xX
cov_yx var_y cov_yz cov_yZ cov_yY cov_yX
cov_zx cov_zy var_z cov_zZ cov_zY cov_zX
cov_Zx cov_Zy cov_Zz var_Z cov_ZY cov_ZX
cov_Yx cov_Yy cov_Yz cov_YZ var_Y cov_YX
cov_Xx cov_Xy cov_Xz cov_XZ cov_XY var_X period(milliseconds)
(36 var/cov values in total + period)To visualize what's going on, we can show samples of a transform as a pose array display in rviz.
rosrun uncertain_tf visualize_samples USAGE: visualize_samples target_frame source_frame num_samples pose_array_topic period(milliseconds)
To make playing around easier, a tf publisher is included that creates a tf tree including a moving turntable.
rosrun uncertain_tf example_tf_tree
Running this, one or more static variance publishers and the visualizer gives a good intuition. As an example, running the folling commands in screens or different consoles, using the same ros master and add a tf tree aswell as a pose array view listening to the topic samples.
rosrun uncertain_tf example_tf_tree rosrun uncertain_tf visualize_samples map object_on_table 1000 smpls 100 rosrun uncertain_tf static_variance_publisher table 0 0 0 0 0 0.5 rosrun uncertain_tf static_variance_publisher turntable 0 0 0 0 0 0.5
Will show a moving toroid structure resulting from the combination of rotational error in the table and the turntable frames:

